|
Na zakończenie cyklu lekcji przeznaczonych dla użytkowników średnio zaawansowanych chciałbym omówić zagadnienie przestrzeni w AutoCAD-zie oraz poruszyć kwestię posługiwania się układami współrzędnych. Przedstawione tu informacje potraktujmy jako wstęp do projektowania w 3D, ponieważ tworzenie w trzech wymiarach wymaga umiejętności sprawnego poruszania się w przestrzeni AutoCAD-a. Najpierw przedstawię podstawowe pojęcia.
Przestrzeń AutoCAD-a jest zbudowana wokół kartezjańskiego układu współrzędnych. Oznacza to, że każdy punkt w przestrzeni posiada trzy współrzędne (X,Y,Z). Do tej pory wszystkie rysowane przez nas projekty były wykonywane w tak zwanym globalnym układzie współrzędnych (GUW). Układ ten jest na stałe związany z rysunkiem i nie może zostać zmieniony przez użytkownika. Do tej pory współrzędna Z była równa 0. GUW jest łatwy do rozpoznania, ponieważ jest oznaczony na rysunku w sposób pokazany poniżej.
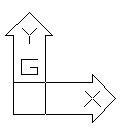
Rys. 1
GUW nie jest jednak jedynym układem współrzędnych, jakiego możemy używać podczas pracy z AutoCAD-em, ponieważ użytkownik może zdefiniować dowolną liczbę własnych układów współrzędnych, zwanych lokalnymi układami współrzędnych (LUW).
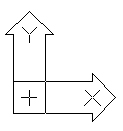
Rys. 2
Każdy z nowo zdefiniowanych lokalnych układów współrzędnych może zostać odpowiednio nazwany, co ułatwia jego identyfikację w systemie oraz łatwe przełączanie się pomiędzy zdefiniowanymi LUW-ami.
Teraz od teorii przejdziemy do praktyki. Proponuję narysowanie kilku elementów na specjalnie do tego celu stworzonych lokalnych układach współrzędnych. Sądzę, że takie rozwiązanie przekona Czytelników do stosowania lokalnych układów współrzędnych podczas pracy z AutoCAD-em w przestrzeni trójwymiarowej. Zacznijmy od narysowania prostego elementu zamkniętego -- radzę wszystkie elementy płaskie, które mają być przekształcane w obiekty 3D, rysować za pomocą polilinii lub, jeśli ktoś woli rysować linią, przekształcać narysowane w ten sposób płaskie elementy w polilinię poleceniem EDPLIN. A zatem narysujmy jakiś niezbyt skomplikowany obiekt -- dziś nie jest naszym celem komplikowanie tworzonych modeli, lecz nauka obsługi układów współrzędnych, ponieważ wiedza, jaką przyswoimy sobie podczas tej lekcji, z pewnością zaowocuje w przyszłości.

Rys. 3
Kolejną czynnością będzie wyświetlenie dwóch pasków narzędzi, które służą do obsługi układów współrzędnych, o nazwach LUW i LUW II.

Rys. 4. LUW

Rys. 5. LUW II
Mając już przygotowane środowisko pracy, stwórzmy układ współrzędnych ulokowany w lewym dolnym narożniku prostokąta. W tym celu klikamy ikonę zwaną LUW
 , ,
po czym w linii poleceń wpisujemy literę N (która oznacza, że chcemy utworzyć nowy lokalny układ współrzędnych), a następnie wskazujemy lewy dolny róg prostokąta. Program w tym miejscu wstawi lokalny układ współrzędnych. Od tej pory w punkcie tym są następujące współrzędne: x=0, y=0, z=0.
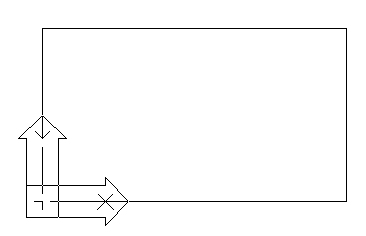
Rys. 6
Układ ten możemy określić jako LUW01. Układ można nazwać za pomocą tej samej ikony -- zamiast klawisza N wciskamy klawisz A (co oznacza Zapisz), a następnie nadajemy naszemu LUW-owi nazwę. Jeśli w tej chwili rozwiniemy okno kliknięciem odpowiedniej ikony na pasku narzędzi LUW II, będziemy mogli zobaczyć, że obok standardowo zdefiniowanych układów powstałych na bazie GUW pojawił się układ nazwany LUW01.
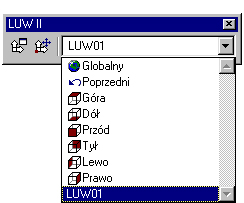
Rys. 7
Teraz za pomocą narzędzia Obrót względem osi X:
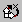
dokonamy obrotu LUW o 90° -- oznaczenie LUW natychmiast zniknie z ekranu, natomiast w lewym dolnym rogu pojawi się następujący znaczek:

Rys. 8
który informuje, że płaszczyzna XY bieżącego układu współrzędnych jest prostopadła do ekranu. Za pomocą narzędzia 3Dorbit możemy obejrzeć nasze dzieło.
Rys. 9
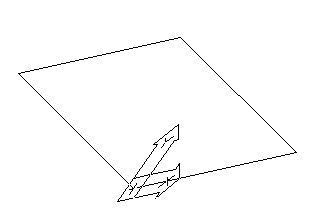
Używając znanych już narzędzi, możemy nazwać nowy LUW jako LUW 02 i narysować kolejny prostokąt lub inny obiekt.
Rys. 10
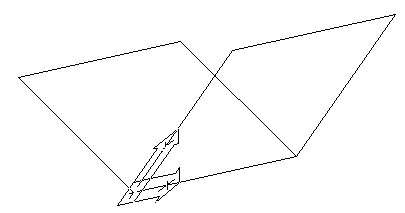
Przy użyciu rozwijanego menu, dostępnego z poziomu paska narzędzi LUW II, możemy się przełączać pomiędzy stworzonymi układami współrzędnych.
Rys. 11
Jak widać, stosowanie LUW-ów umożliwia definiowanie osobnych układów współrzędnych dla poszczególnych płaszczyzn konstrukcyjnych, co wraz z nadawaniem im odpowiednich nazw znacznie skraca czas projektowania. Lokalne układy współrzędnych można również stosować podczas tworzenia rysunków płaskich, np. w celu obrócenia układu współrzędnych o 45°.
Mam nadzieję, że niniejsza lekcja, ostatnia z cyklu dla średnio zaawansowanych, rozbudziła apetyty Czytelników na lekcje następne. W kolejnym cyklu lekcji zostaną przedstawione techniki i sposoby tworzenia modeli w przestrzeni trójwymiarowej.
[Poprzednia lekcja]
[Spis treści]
Krystian Kapias, © Wydawnictwo Helion 2001.
|






