|
Grafy puste składają się jedynie z wierzchołków, nie zawierają
źadnych krawędzi.
Graf pusty o n wierzchołkach oznaczamy Nn.
 
 
  |
|
Grafy puste
mają następujące własności:
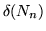
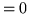 , ,
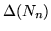
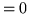 , ,
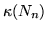
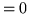 , ,
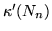
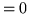 , ,
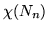
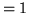 , ,
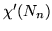
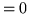 , ,
Cykl Hamiltona: nie posiadają.
Cykl Eulera: nie posiadają.
Są planarne.
Spróbuj zastanowić się, dlaczego tak jest. |
|
|
|
Grafy pełne to grafy, w których każde dwa wierzchołki są połączone
krawędzią. Graf pełny o 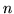 wierzchołkach oznaczamy
wierzchołkach oznaczamy 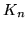 . .
 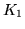
 
 
 |
|
Grafy pełne o
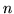 wierzchołkach mają następujące własności:
wierzchołkach mają następujące własności:
Mają 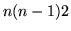 krawędzi.
krawędzi.
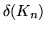
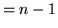 , ,
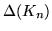
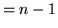 , ,
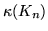
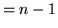 , ,
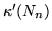
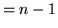 , ,
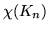
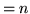 , ,
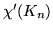
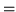
 |
| dla n
nieparz. n>1 |
| dla n
parzystych |
|
Cykl Hamiltona: posiadają.
Cykl Eulera: posiadają jeśli 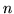 jest nieparzyste.
jest nieparzyste.
Są planarne tylko dla 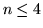 . .
Spróbuj zastanowić się, dlaczego tak jest. |
|
|
|
Grafy pełne dwudzielne to grafy dwudzielne, które zawierają
wszystkie możliwe krawędzie przy zadanym podziale zbioru wierzchołków.
Graf pełny dwudzielny, którego wierzchołki podzielone są na zbiór 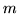 elementowy i
elementowy i 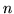 elementowy
oznaczamy elementowy
oznaczamy 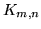 . .
 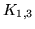
 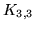
 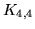
 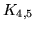
|
|
Grafy pełne
dwudzielne o 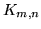 mają następujące własności:
mają następujące własności:
Mają 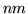 krawędzi.
krawędzi.
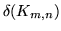
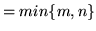 , ,
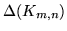
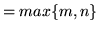 , ,
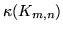
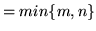 , ,
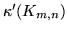
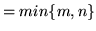 , ,
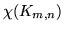
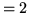 , ,
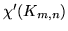
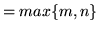 , ,
Cykl Hamiltona: posiadają jeśli 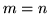 . .
Cykl Eulera: posiadają jeśli 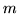 i
i 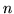 są parzyste.
są parzyste.
Są planarne tylko dla dla 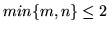 . .
Spróbuj zastanowić się, dlaczego tak jest. |
|
|
|
W 1930 roku polski matematyk Kazimierz Kuratowski udowodnił, że
najmniejsze grafy nieplanarne to 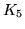 i
i 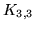 , oraz że
grafy nieplanarne to tylko te, które w pewien sposób zawierają któryś z
tych dwóch grafów. , oraz że
grafy nieplanarne to tylko te, które w pewien sposób zawierają któryś z
tych dwóch grafów.
Litera "K" w oznaczeniu grafów pełnych pochodzi właśnie od jego
nazwiska, a grafy 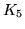 i i 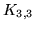 często nazywa się grafami Kuratowskiego
często nazywa się grafami Kuratowskiego
Koła to grafy powstałe przez dodanie do cyklu jeszcze jednego
wierzchołka i połączenie tego wierzchołka ze wszystkimi wierzchołkami
cyklu.
Koło o 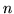 wierzchołkach
oznaczamy wierzchołkach
oznaczamy 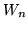 . .
Drzewa to grafy spójne nie zawierające żadnego cyklu.
Istnieje wiele różnych (nieizomorficznych) drzew o tej samej liczbie
wierzchołków. Oto przykłady drzew o 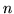 wierzchołkach.
wierzchołkach.
Graf, którego każda składowa jest drzewem nazywamy lasem. Oto
przykład lasu:

Grafy platońskie to grafy utworzone z krawędzi i wierzchołków
wielościanów foremnych.
czworościan: sześcian: sześcian:
ośmiościan:
dwunastościan:
dwudziestościan:
O wielościanach foremnych wspomina też wykład z Algebry. A miniprogram
pozwala na bliższe zaznajomienie się z nimi.
Wszystkie grafy platońskie są regularne i planarne.
Łatwo można się przekonać, że grafy platońskie spełniają formułę
Eulera, którą możemy zapisać:
gdzie 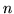 oznacza liczbę
wierzchołków grafu, oznacza liczbę
wierzchołków grafu, 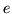 liczbę krawędzi, a
liczbę krawędzi, a 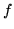 liczbę obszarów grafu. Przez obszary rozumiemy obszary spójne, na które
dzielą płaszczyznę krawędzie grafu narysowanego na tej płaszczyżnie. (Dla
bryły będą to po prostu jej ściany). Należy pamiętać przy tym, żeby
policzyć też "obszar nieskończony", czyli "zewnętrze"
grafu.
liczbę obszarów grafu. Przez obszary rozumiemy obszary spójne, na które
dzielą płaszczyznę krawędzie grafu narysowanego na tej płaszczyżnie. (Dla
bryły będą to po prostu jej ściany). Należy pamiętać przy tym, żeby
policzyć też "obszar nieskończony", czyli "zewnętrze"
grafu.
Formułę Eulera spełniają wszystkie grafy planarne narysowane w ten sposób,
że ich krawędzie nie przecinają się.
Graf Petersena:
Graf Grötzscha:

|
